View as Slides

3D Data Visualization Workshop

Deborah Schmidt
Head of Helmholtz Imaging Support Unit, MDC Berlin
Sep 17, 2025
Slides available at https://ida-mdc.github.io/workshop-visualization/1-2_introduction-3d-data-types/

3D Dataset types

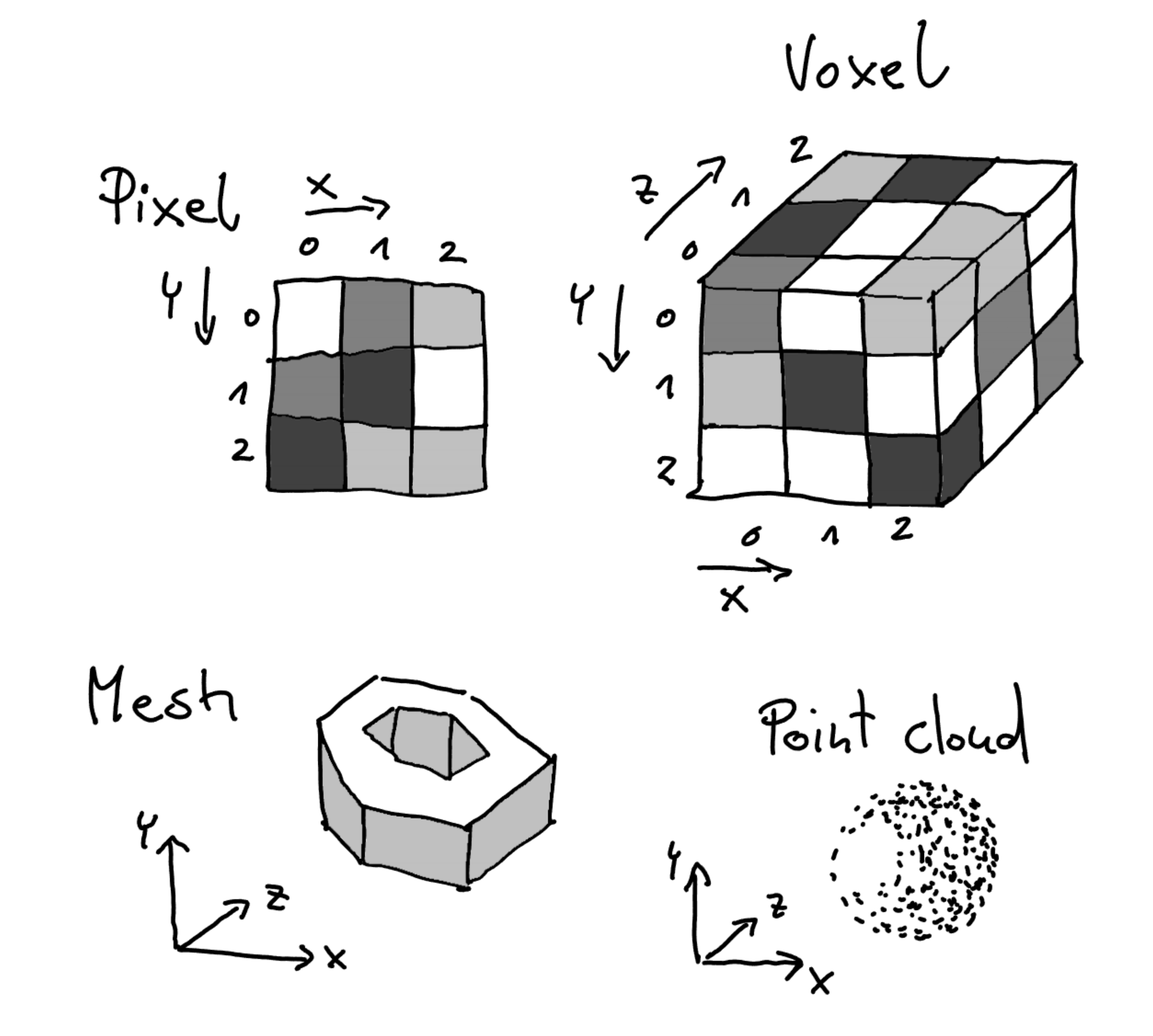
  • Voxel-Based Datasets (Euclidean-structured)
  • Meshes (Non-Euclidean-structured)
  • Point Clouds (Non-Euclidean-structured)
  • Vector Fields (structured or unstructured)

Voxel‑Based Images

  • What is it? 3D grid (voxels) with scalar (or vector/tensor) values.
  • Acquire (by domain): CT/MRI, light‑sheet/confocal, micro‑CT, simulations.
  • Used for: Inspect interiors, segment/analyze regions, measure volumes.
  • Stored as: TIFF stacks, NIfTI/NRRD, HDF5, OME‑Zarr (great for big data & web).
  • Visualized with: Orthogonal slices, volume ray casting, MIP, isosurfaces.
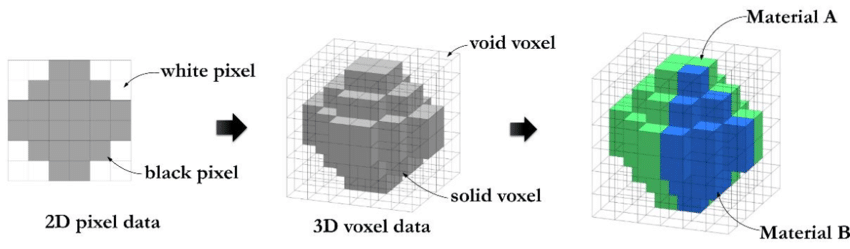
Voxel based data representation. Credit: Hasanov, S. et al. (2021), CC BY-SA 4.0.

Voxel based data representation. Credit: Hasanov, S. et al. (2021), CC BY-SA 4.0.

Voxel‑Based Images

Voxel spacing, anisotropy

  • Spacing = physical size per voxel (e.g., 0.2 × 0.2 × 1.0 µm).
  • Isotropic: spacing equal along axes → cubes; anisotropic: one axis differs (common in microscopy & clinical CT).
  • Always set spacing in your viewer/exporter.
    • In napari, set “Scale” in layer properties.
    • In VTK/ParaView, set “Data Spacing” or use image origin/spacing fields.
  • Resample if needed (trade speed vs fidelity): upsample Z for nicer isosurfaces; downsample big XY for faster previews.

Voxel‑Based Images

Visualizing volumetric datasets

  • Slice‑based: axial/sagittal/coronal (medical) or arbitrary oblique slices.
  • Maximum/Minimum Intensity Projections (MIP/MinIP): great for vessels or bright structures.
  • Emission‑absorption (volume ray casting): assign color + opacity by intensity (“transfer function”); can add lighting.
  • Isosurface: fast surface extraction at a threshold (marching cubes) for clean boundaries.
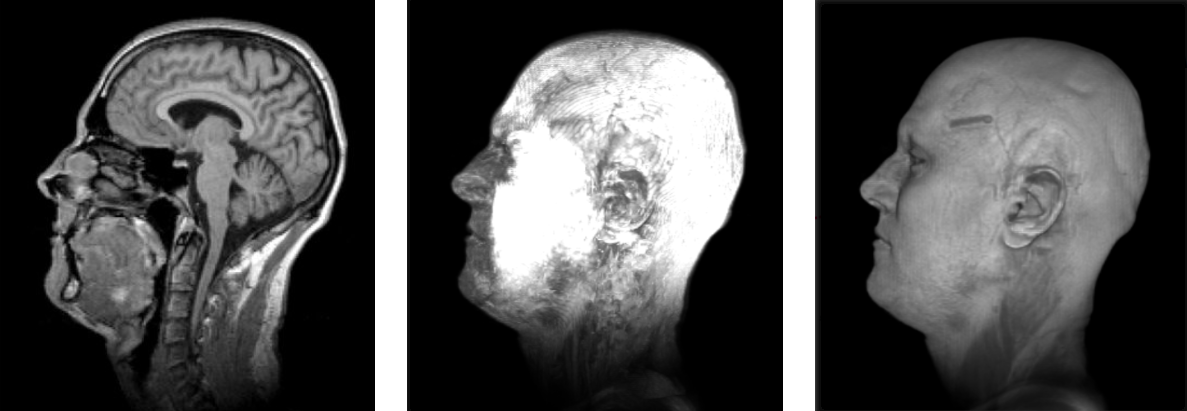
Slicing, Max. Intensity, Emission Absorbtion

Slicing, Max. Intensity, Emission Absorbtion

Thetawavederivative work: Florian Hofmann, CC BY-SA 3.0

Thetawavederivative work: Florian Hofmann, CC BY-SA 3.0

Voxel‑Based Images

Volume Rendering in napari

  • Interactive visualization and annotation: Offers tools for exploring data and annotating images in real-time.
  • Layer-based rendering: Supports multiple layers like images, labels, points, and shapes for versatile data representation.
  • Plugin extensibility: Easily extendable through plugins to add custom functionality.
  • Integration with Python ecosystem: Seamlessly works with NumPy, Dask, and other scientific Python libraries.

Voxel‑Based Images

Praxis: Visualizing volumes with napari

  1. Open napari → File → Open… a 3D stack (TIFF/OME‑TIFF/NIfTI/Zarr).
  2. In the Layers panel, select your image layer:
    • Set Scale to the correct voxel spacing (e.g., 0.2, 0.2, 1.0).
    • Switch 2D → 3D (bottom left bar).
    • In Rendering, try: MIP, Translucent/Attenuated, Iso.
  3. Adjust the contrast limits and colormap; add a labels layer if you have a segmentation.
  4. File → Save Screenshot to export a figure (optionally with a transparent background).

Photogrammetry

Jan-Simon Schmidt (HZB), Ole Johannsen (DKFZ, Helmholtz Imaging), Deborah Schmidt (MDC, Helmholtz Imaging)

Photogrammetry

  • What is it? Recover camera poses (SfM) → compute depth (MVS) → output dense point cloud and mesh+texture.
  • Acquire (by domain): Drone surveys, cultural heritage, lab setups; consistent overlap & fixed focal preferred.
  • Used for: Reconstruction, measurement, communication, web sharing.
  • Stored as: Images + camera models, PLY/OBJ/GLB mesh, LAS/PLY point cloud, optional orthomosaics/DEMs.
  • Visualized with: Mesh or point‑based viewers; geospatial tools when georeferenced.

Point clouds

  • What is it? A set of 3D points with attributes (intensity, color, class, time…).
  • Acquire (by domain):
    • LiDAR (ground/airborne), depth sensors.
    • Photogrammetry (dense matching).
    • Microscopy (particle centers, single‑molecule localizations).
  • Used for: Mapping, fitting, statistics, reconstruction.
  • Stored as: LAS/LAZ, E57, PLY, CSV/Parquet; for the web: EPT (Entwine Point Tiles).
  • Visualized with: Point rendering (“Point Gaussian”), color by attribute, subsampling & LODs.

Point clouds

Rendering challenges

  • No connectivity → consider surface reconstruction (e.g., Poisson, alpha‑shapes) when needed.
  • Often noisy & redundant → filter, align, downsample, and normalize intensities.
Aldino Rizaldy, Sam Thiele, Sharad Kumar Gupta, HZDR

Point Clouds

Domain-Specific Variants

  • Many scientific domains represent data as points in 3D space with domain-specific attributes.
    • Atoms in molecules → standardized formats (PDB, mmCIF), rendered as spheres/bonds
    • Stars in astronomy → catalogs (FITS, VOTable), rendered as brightness-colored points
    • Cells in microscopy → tables or SWC/OME formats, rendered as centroids or markers
  • Same principles apply, but with tailored formats & rendering techniques

Point clouds

Praxis: Visualizing point clouds with ParaView

  1. File → Open… a LAS/LAZ/PLY or CSV with XYZ.

  2. Click Apply. In the Properties panel:

    • Set Representation = Point Gaussian for smooth points.
    • Increase Gaussian Radius until points visually connect.

Point clouds

Praxis: Visualizing point clouds with ParaView

  1. Add filters as needed (Filters → Search):

    • Clip (box/plane) to isolate a region.
    • Decimate (Points) or Mask Points to downsample for speed.

  2. Save a screenshot or File → Export Scene for vector graphics.

Meshes

  • What is it? Vertices + faces define a continuous surface.
  • Acquire (by domain): From segmentation (marching cubes), CAD, photogrammetry, simulation output.
  • Used for: Visualization, 3D printing, analysis (curvature/area), animation.
  • Stored as: STL, PLY, OBJ, GLB/GLTF, VTP; textures as PNG/JPEG; materials in MTL/GLTF.
  • Visualized with: Smooth shading, PBR materials (Physically-Based Rendering, for textured assets), scalar maps, cuts/slices.

Mesh processing

Tools

  • MeshLab: A powerful tool for cleaning, decimating, and refining 3D meshes. It supports:

    • Smoothing: Remove sharp edges or rough areas in the mesh.
    • Decimation: Reduce the number of polygons while maintaining the overall shape.
    • Repair: Fix holes or non-manifold geometry in the mesh for better usability.

  • Other tools: Blender and VTK also offer additional mesh processing capabilities.

Rendering meshes

Meshes

Rendering pipeline

  • Vertex shader: places points in the scene.
  • Geometry (optional): can add/quench primitives.
  • Fragment shader: colors pixels using lights/materials/textures.
  • Depth & blending: decide what’s in front and how transparent things mix.
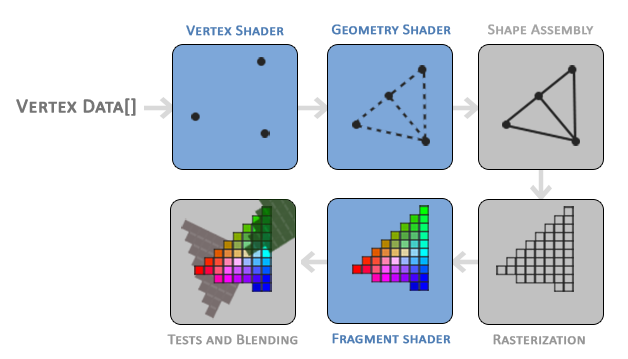
Credit: Joey de Vries,https://learnopengl.com/, CC BY 4.0

Credit: Joey de Vries,https://learnopengl.com/, CC BY 4.0

Meshes

Praxis: Visualizing meshes with ParaView

  1. File → Open… a mesh → Apply.
  2. Lighting/shading: set Representation = Surface.

Vector fields

Grids and unstructured meshes

  • What is it? A vector (ux,uy,uz) per location; often paired with scalars (pressure, temperature).
  • Acquire (by domain): CFD/FEA, climate/ocean models, MRI‑flow, EM fields.
  • Used for: Flow direction/speed, vortices, transport, streamline topology.
  • Stored as:
    • Structured grids: VTI/NetCDF/XDMF+HDF5; rectilinear or curvilinear coordinates.
    • Unstructured: VTU/VTK with per‑point or per‑cell vector arrays.

Vector fields

Grids and unstructured meshes

  • Visualized with:
    • Glyphs (arrows/cones) scaled by magnitude.
    • Streamlines (steady) or pathlines/particle tracers (time‑varying).

Vector fields

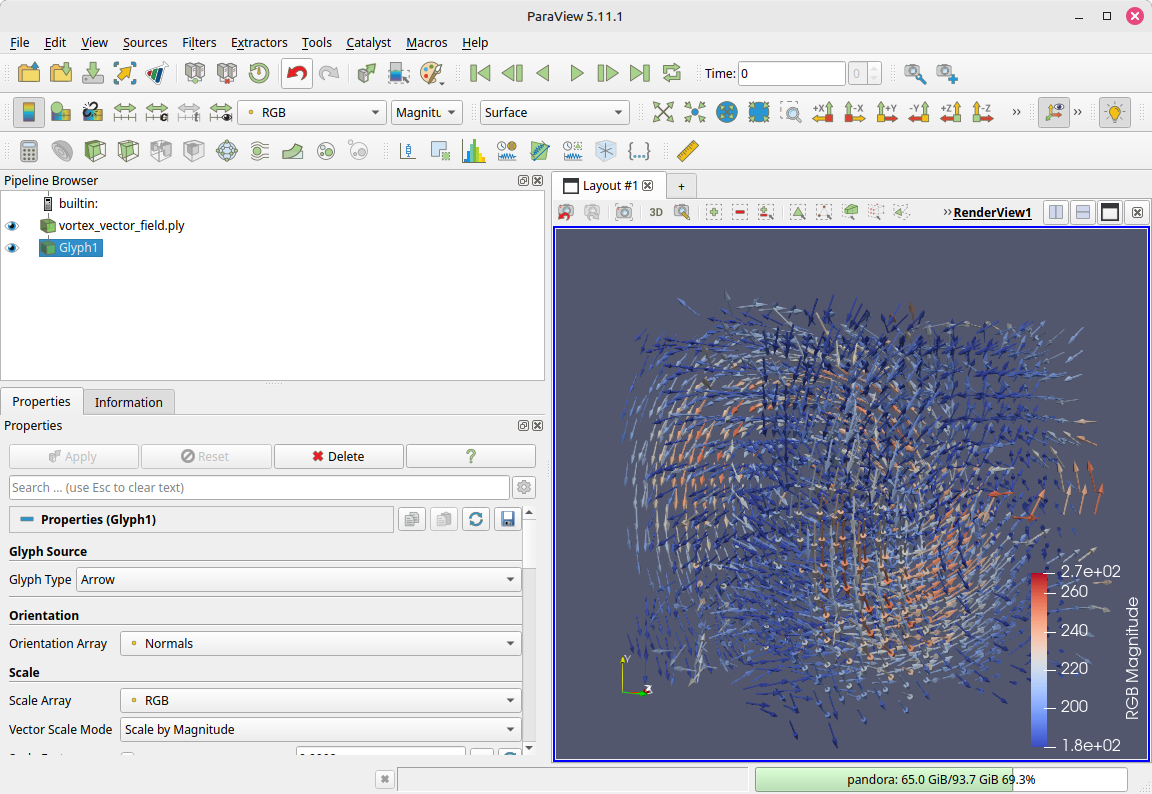
Praxis: Visualizing vector fields with ParaView

  1. File → Open… a VTK/VTU/VTI/XDMF/NetCDF file with vectors → Apply.

  2. Glyphs: Filters → Glyph.

    • Vectors = your vector array (e.g., Velocity).
    • Scale by = vector magnitude; set a sensible Scale Factor.
    • Pick Glyph Type = Arrow (or Cone) → Apply.

It’s your turn!

  • open Napari to look at 3D Pixel data
  • open Paraview to look at Meshes, Point Clouds, and Vector Fields
2025 | HELMHOLTZ IMAGINGExit slides